Μια νέα εργασία απέδειξε ένα ερώτημα στη Θεωρία Γράφων που απασχολεί εδώ και δεκαετίας τους μαθηματικούς, που ασχολούνται με το πεδίο που λέγεται Συνδυαστική. Το ερώτημα αφορά τους λεγόμενους αριθμούς Ramsey, αλλά είναι πιο γνωστό ως «πρόβλημα του πάρτι».
Γενικά μιλώντας, οι αριθμοί Ramsey είναι μεγέθη που αντικατοπτρίζουν τα όρια μιας πιθανής διαταραχής. Πιο συγκεκριμένα, αυτοί οι αριθμοί μετρούν το μέγεθος που μπορούν να αποκτήσουν οι συλλογές κορυφών και ακμών, που ονομάζονται γράφοι ή γραφήματα, προτού αναπόφευκτα εμφανίσουν κάποιο μοτίβο ή δομή.
Ο σχεδιασμός ενός πάρτι συναντά τη θεωρία γραφημάτων
Για να καταλάβετε τι είναι ο αριθμός Ramsey, φανταστείτε ότι διοργανώνετε ένα πάρτι. Πόσα άτομα θα πρέπει να προσκαλέσετε για να είστε σίγουροι ότι θα υπάρχει μια ομάδα ανθρώπων που όλοι γνωρίζονται μεταξύ τους ή μια ομάδα που είναι όλοι άγνωστοι;
Μπορείτε να κωδικοποιήσετε αυτό το ερώτημα στη γλώσσα των γραφημάτων. Αναθέστε μια κορυφή σε κάθε άτομο. Έτσι, για $n$ καλεσμένους, έχετε $n$ κορυφές. Συνδέστε κάθε ζεύγος κορυφών με μια ακμή. Έπειτα, χρωματίστε κάθε ακμή κόκκινη, αν τα άτομα γνωρίζονται ήδη μεταξύ τους, αλλά χρωματίστε την μπλε αν δε γνωρίζονται καθόλου. Έτσι όλες οι ακμές θα είναι είτε κόκκινες (γνωστοί) είτε μπλε (άγνωστοι).
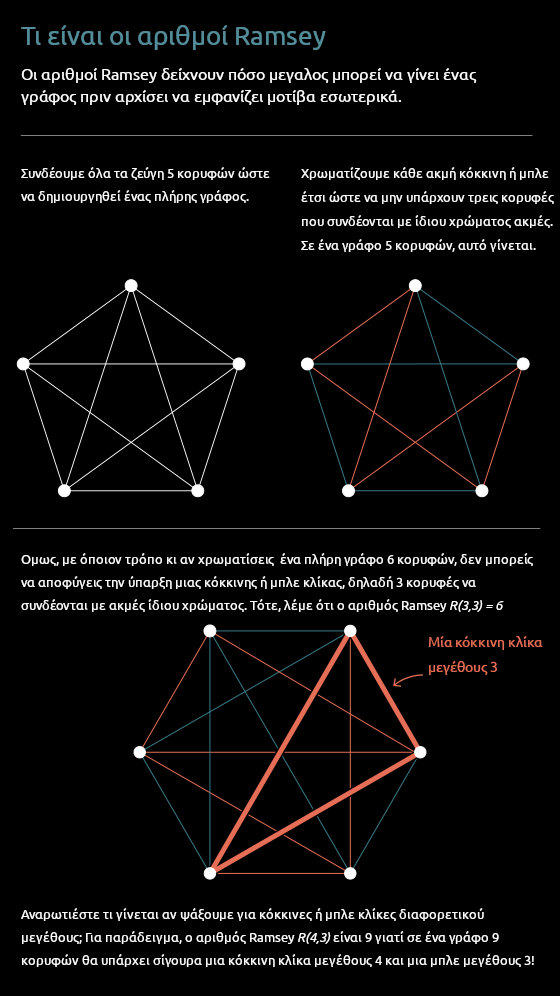
Στα μαθηματικά της Θεωρίας Γράφων, μια ομάδα κοινών γνωστών ή αγνώστων αντιπροσωπεύεται από μια δομή που ονομάζεται κλίκα: ένα σύνολο κορυφών που συνδέονται με ακμές του ίδιου χρώματος. Ο αριθμός Ramsey $R(s, t)$ είναι ο ελάχιστος αριθμός ατόμων που πρέπει να προσκαλέσετε στο πάρτι σας για να υπάρχει σίγουρα μια υποομάδα από τουλάχιστον $s$ γνωστά μεταξύ τους άτομα ή μια ομάδα από $t$ εντελώς αγνώστους μεταξύ τους. Στη γλώσσα της θεωρίας γραφημάτων, το R είναι ο ελάχιστος αριθμός κορυφών που πρέπει να έχει ένα γράφημα ώστε να περιλαμβάνει είτε μια κόκκινη κλίκα μεγέθους $s$ ή μια μπλε κλίκα μεγέθους $t$. Μάλιστα, το θεώρημα του Ramsey, λέει ότι υπάρχει πάντα ένας τέτοιος αριθμός R για κάθε s, t.
Για παράδειγμα, γνωρίζουμε ότι $R(4, 5) = 25$. Δηλαδή, μπορείτε να διοργανώσετε ένα πάρτι με 24 άτομα, μερικά από τα οποία γνωρίζονται μεταξύ τους, χωρίς να υπάρχει ούτε μια ομάδα τεσσάρων κοινών γνωστών ή πέντε αγνώστων! Αλλά αν προσθέσετε ένα ακόμη άτομο, δεν μπορείτε να αποφύγετε τη δημιουργία τουλάχιστον μιας από αυτές τις δομές.
Νωρίτερα φέτος, μια από τις ανακαλύψεις στη συνδυαστική έδωσε ένα αυστηρότερο άνω όριο για τους "συμμετρικούς" αριθμούς Ramsey $R(t,t)$ ή για συντομία $R(t)$, όπου οι κόκκινες και οι μπλε κλίκες έχουν το ίδιο μέγεθος. Με τους ασύμμετρους αριθμούς Ramsey - το αντικείμενο του νέου αποτελέσματος - οι μαθηματικοί καθορίζουν το μέγεθος της κόκκινης κλίκας (γνωστοί) για να μελετήσουν τι συμβαίνει όταν το μέγεθος της μπλε κλίκας (άγνωστα μεταξύ τους άτομα) γίνεται αυθαίρετα μεγάλο.
Οι μαθηματικοί έχουν καταφέρει να υπολογίσουν με ακρίβεια μόνο μια χούφτα από τους μικρότερους αριθμούς Ράμσεϊ αυτής της κατηγορίας. Το 1995 απέδειξαν ότι $R(4, 5) = 25$. Κανείς όμως δε γνωρίζει την τιμή του $R(4, 6)$. Ομοίως, στις αρχές της δεκαετίας του 1980, έδειξαν ότι $R(3, 9) = 36$, αλλά το $R(3, 10)$ παραμένει ένα ανοιχτό πρόβλημα. Η συμμετρική περίπτωση είναι εξίσου δύσκολη: $R(4) = 18$, αλλά η ακριβής τιμή του $R(5)$ δεν είναι γνωστή.
Και έτσι, αφού δεν μπορούν να τους υπολογίσουν επακριβώς, οι μαθηματικοί προσπαθούν να «εκτιμήσουν» τους αριθμούς Ramsey, δηλαδή να υπολογίσουν ανώτερα και κατώτερα όρια για τις τιμές τους. Στη δεκαετία του 1990, οι ερευνητές χρησιμοποίησαν τεχνικές για την τυχαία δημιουργία γραφημάτων για να αποδείξουν ότι αν η κόκκινη κλίκα είναι σταθερή στο 3 και η μπλε γίνεται όλο και μεγαλύτερη, το μέγεθος του αριθμού Ramsey αυξάνεται ως το τετράγωνο του μεγέθους της μπλε κλίκας - για την ακρίβεια $ R(3,t) = Ω (\frac{t^2} {log{t}} ) $ καθώς $t \rightarrow \infty $. Μπορείτε να δείτε μια λίστα με τους γνωστούς αριθμούς Ramsey και τα κατώτερα-ανώτερα όριά τους στο https://mathworld.wolfram.com/RamseyNumber.html
Η νέα απόδειξη, που δημοσιεύτηκε στο διαδίκτυο τον Ιούνιο, διερωτάται τι συμβαίνει όταν το μέγεθος της κόκκινης κλίκας ορίζεται σε 4 αντί για 3. Στη δεκαετία του 1930, διαπιστώθηκε ότι το $R(4, t)$ δεν αυξάνεται γρηγορότερα από περίπου $t^3$. Αλλά το καλύτερο κατώτερο όριο, που βρέθηκε τη δεκαετία του 1970, είναι περίπου $t^{{5}/{2}}$ - σημαντικά μικρότερο.Οι προσπάθειες να καλυφθεί το χάσμα αυξάνοντας το κατώτερο όριο ή μειώνοντας το ανώτερο απέτυχαν επί δεκαετίες, μέχρι τώρα που δύο μαθηματικοί πρόσθεσαν ένα βασικό συστατικό καθώς απέδειξαν είναι ότι:
$$ R(4,t) = Ω \left( \frac{t^3} {log^4{t}} \right) $$ καθώς $t \rightarrow \infty $
Το ενδιαφέρον της νέας απόδειξης είναι ότι σηματοδοτεί μια απόκλιση από τις μέχρι τώρα τεχνικές που χρησιμοποιούν οι μαθηματικοί. Όχι μόνο λύνει ένα πρόβλημα που «αντιστεκόταν» για περισσότερα από 40 χρόνια, αλλά παρουσιάζει επίσης έναν νέο οδικό χάρτη για το πώς οι μαθηματικοί θα μπορούσαν να αντιμετωπίσουν τα προβλήματα σχετικά με τους αριθμούς Ramsey στο μέλλον.
Κρυμμένο σε κοινή θέα
Το 2019, ο Sam Mattheus, τότε μεταπτυχιακός φοιτητής στο Ελεύθερο Πανεπιστήμιο των Βρυξελλών (VUB), αναζητούσε έμπνευση. Η ειδικότητά του ήταν η πεπερασμένη γεωμετρία, η μελέτη των διατάξεων σημείων, γραμμών και άλλων δομών σε ειδικά καθορισμένους χώρους. Αλλά παρόλο που βρήκε το έργο ενδιαφέρον, ένιωθε να περιορίζεται από το πόσο αυστηρές και ακριβείς έπρεπε να είναι αυτές οι γεωμετρικές κατασκευές.
Στη συνέχεια είδε μια εργασία από δύο μαθηματικούς, τον Dhruv Mubayi από το Πανεπιστήμιο του Ιλινόις, στο Σικάγο και τον Jacques Verstraete από το Πανεπιστήμιο της Καλιφόρνια, στο Σαν Ντιέγκο (UCSD). Ξανασκέφτονταν πώς να προσεγγίσουν τα προβλήματα Ramsey. Ενώ οι παραδοσιακές τεχνικές περιλαμβάνουν την τυχαία δημιουργία γραφημάτων για να λάβουν καλές εκτιμήσεις των αριθμών Ramsey, οι Mubayi και Verstraete ξεκίνησαν με «ψευδοτυχαίες» κατασκευές που φαίνονται τυχαίες, αλλά δεν είναι.
Κάτι έκανε κλικ στον Mattheus. Ίσως, σκέφτηκε, η γεωμετρική του προοπτική θα μπορούσε να βοηθήσει. Για τα επόμενα δύο χρόνια, ενώ ολοκλήρωνε τις μεταπτυχιακές του εργασίες, είχε αυτή την ιδέα στο πίσω μέρος του μυαλού του. Στη συνέχεια υπέβαλε αίτηση για υποτροφία Fulbright, η οποία θα του επέτρεπε να συνεχίσει ένα μεταδιδακτορικό πρόγραμμα με τον Verstraete στις ΗΠΑ.
Το 2022, λίγο αφότου ο Mattheus έλαβε το βραβείο Fulbright (μαζί με μια άλλη υποτροφία), μετακόμισε στο UCSD και άρχισε να εργάζεται με τον Verstraete στο $R(4,t)$. Οι δύο μαθηματικοί ήθελαν να αυξήσουν το κατώτερο όριο για να πλησιάσουν περισσότερο στο γνωστό ανώτερο όριο. Για να το κάνουν αυτό, θα πρέπει να βρουν ένα γράφημα με σχεδόν $t^3$ κορυφές που να μην έχει κόκκινες κλίκες μεγέθους 4 ή μπλε κλίκες μεγέθους $t$. Για να λειτουργήσουν οι αποδείξεις τους, αναδιατύπωσαν το πρόβλημα. Φανταστείτε απλώς να διαγράψετε κάθε μπλε άκρη. Ο στόχος είναι τώρα να βρεθεί ένα γράφημα χωρίς κόκκινες κλίκες μεγέθους 4, και χωρίς ανεξάρτητα σύνολα μεγέθους $t$ (δηλαδή, σύνολα κορυφών $t$ χωρίς ακμές).
Η εργασία των Mubayi και Verstraete το 2019 υπονοούσε ότι αν μπορείτε να κατασκευάσετε ένα ψευδοτυχαίο γράφημα χωρίς κόκκινες κλίκες μεγέθους 4, τότε μπορείτε να πάρετε τυχαία κομμάτια του για να λάβετε μικρότερα γραφήματα χωρίς μεγάλα ανεξάρτητα σύνολα. Αυτό ακριβώς ήθελαν να βρουν ο Mattheus και ο Verstraete. Ξεκινώντας με ένα ακόμη μεγαλύτερο γράφημα, ήλπιζαν να βρουν ένα γράφημα με σχεδόν $t^3$ κορυφές που να πληρούσε τα κριτήριά τους.
Το πρόβλημα ήταν να βρουν τη σωστή ψευδοτυχαία κατασκευή για να ξεκινήσουν. Για να το πετύχουν, έπρεπε να φτάσουν εκεί με έναν κάπως καινοτόμο τρόπο. Δεν ξεκίνησαν με ένα ψευδοτυχαίο γράφημα. Δεν ξεκίνησαν καθόλου με ένα γράφημα. Αντίθετα, ο Mattheus θυμήθηκε ένα παράξενο αντικείμενο που ονομάζεται Ερμιτική μονάδα, κάτι με το οποίο οι γεωμέτρες τείνουν να είναι πολύ εξοικειωμένοι - αλλά που ένας μαθηματικός που εργάζεται στη συνδυαστική ήταν απίθανο να συναντήσει ποτέ.
Μια ερμητική μονάδα είναι ένα ειδικό σύνολο σημείων σε μια καμπύλη, μαζί με γραμμές που διέρχονται από αυτά τα σημεία σε συγκεκριμένες διαμορφώσεις. Είναι πολύ σημαντικό ότι μπορεί επίσης να αναπαρασταθεί ως ένα γράφημα που αποτελείται από πολλές μεγάλες αλλά ελάχιστα επικαλυπτόμενες κλίκες. Αυτό το γράφημα είναι πολύ γνωστό και πολλές από τις ιδιότητές του έχουν μελετηθεί. Αλλά ποτέ δεν είχε ληφθεί υπόψη στο πλαίσιο των προβλημάτων Ramsey.
Το γράφημα μπορεί να μη φαίνεται χρήσιμο με την πρώτη ματιά, καθώς περιέχει τόσες πολλές μεγάλες κλίκες. Αλλά ένα βασικό χαρακτηριστικό της ερμητικής μονάδας είναι ότι περιέχει μόνο κλίκες μεγέθους 4 των οποίων οι κορυφές συγκεντρώνονται μαζί με άτυπο τρόπο. Λόγω αυτής της ιδιότητας, ήταν σχετικά εύκολο για τους δύο μαθηματικούς να καταστρέψουν αυτές τις ανεπιθύμητες κλίκες διαγράφοντας τυχαία άκρες.
Αυτές οι διαγραφές τους έδωσαν ένα νέο γράφημα χωρίς κλίκες μεγέθους 4 — αλλά παρόλα αυτά περιείχε μεγάλα ανεξάρτητα σύνολα. Ο Mattheus και ο Verstraete έπρεπε τώρα να αποδείξουν ότι αυτό το γράφημα ήταν ψευδοτυχαίο. Με αυτόν τον τρόπο, κατάφεραν τελικά να χρησιμοποιήσουν την απόδειξη του 2019 όπως ήλπιζαν. Πήραν τυχαίους υπογράφους με περίπου $t^3$ κορυφές και μπορούσαν να εγγυηθούν ότι αυτοί οι υπογράφοι δεν είχαν ανεξάρτητα σύνολα μεγέθους $t$.
Αυτό ολοκλήρωσε την απόδειξη. Αυτή η κατασκευή είναι όμορφη και προαναγγέλλει μια αλλαγή στον τρόπο με τον οποίο οι μαθηματικοί σκέφτονται για τα προβλήματα Ramsey.
