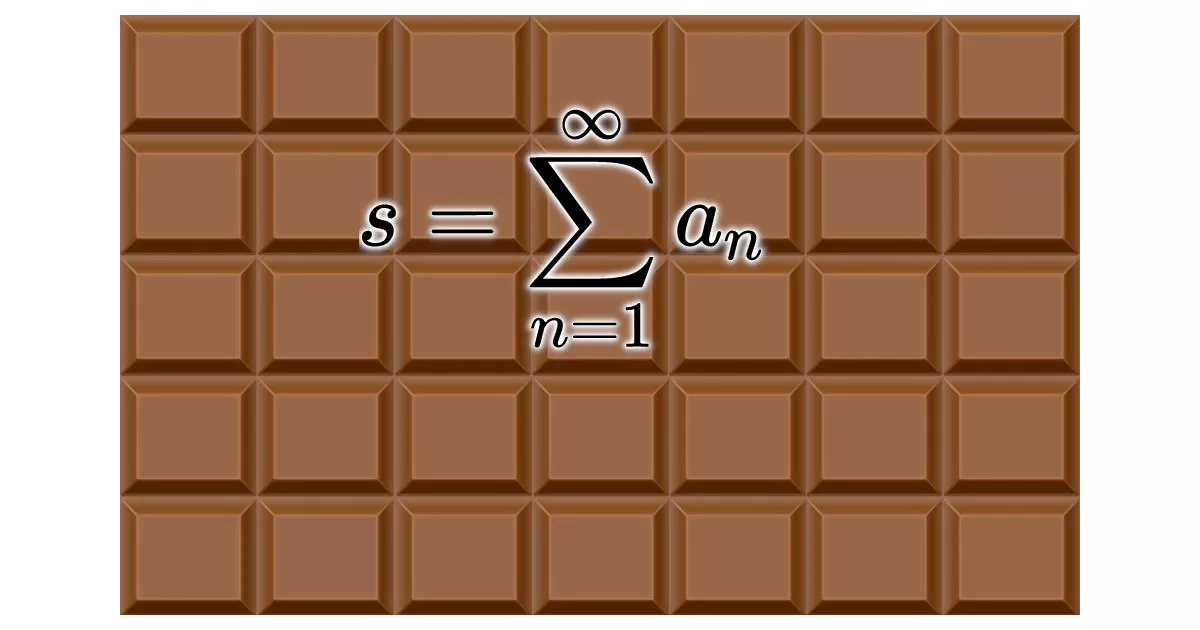
Το σπουδαίο με τα μαθηματικά είναι ότι μπορούν να αντιμετωπίσουν την περίπλοκη έννοια του απείρου. Ένα παράδειγμα αυτού προέρχεται από τα άπειρα αθροίσματα, γνωστά και ως άπειρες σειρές.
Πάρτε για παράδειγμα αυτό εδώ το άθροισμα: $\frac{1}{4}+\frac{1}{16}+\frac{1}{64} + \cdots $
Όπως υποδηλώνουν οι τελείες, η σειρά συνεχίζεται για πάντα, ή όπως λέμε "έχει άπειρους όρους". Στη συγκεκριμένη σειρά, κάθε νέος όρος είναι ένα κλάσμα το οποίο είναι τέσσερις φορές μικρότερο από τον προηγούμενο όρο. Τα κλάσματα αυτά συνεχίζονται επ' άπειρον, αλλά το "άθροισμα" τους είναι πεπερασμένο και, στην πραγματικότητα, είναι ίσο με $\frac{1}{3}$. Δηλαδή, ισχύει το εξής:
$\frac{1}{4}+\frac{1}{16}+\frac{1}{64} + \cdots = \frac{1}{3} $
ή όπως θα έγραφε ένας μαθηματικός για να κάνει επίδειξη (μην τρομάξετε, είναι το ίδιο πράγμα):
$\sum_{n=1}^{\infty} \frac{1}{ 4 ^ n } = \frac{1}{3}$
Ας το αποδείξουμε τώρα αυτό με έναν ελαφρώς αντισυμβατικό τρόπο, χρησιμοποιώντας σοκολάτα!
Φανταστείτε, αν θέλετε, ότι είστε καταστηματάρχης και πουλάτε σοκολάτες με την παρακάτω ειδική προσφορά:
- Σε κάθε μπάρα σοκολάτας, υπάρχει ένα κουπόνι.
- Συλλέξτε 4 κουπόνια και πάρτε δωρεάν μια μπάρα σοκολάτας.
Δηλαδή, κάθε μπάρα περιέχει $1$ μονάδα πραγματικής σοκολάτας αλλά και $1$ κουπόνι. Έτσι, ένας πελάτης με $4$ κουπόνια μπορεί να διεκδικήσει $1$ μπάρα δωρεάν. Το κλειδί για την απόδειξη του αποτελέσματός μας είναι η ακόλουθη ερώτηση:
Πόσο αξίζει ένα κουπόνι, σε όρους πραγματικής σοκολάτας;
Υπολογίζοντας μιαν άπειρη σειρά
Λοιπόν, $4$ κουπόνια αξίζουν $1$ μπάρα και επομένως $1$ κουπόνι αξίζει, κατά μία έννοια, $\frac{1}{4}$ της μπάρας. Ομως, η μπάρα έχει μέσα σοκολάτα και κουπόνι. Έτσι, $1$ κουπόνι αξίζει:
$\frac{1}{4} \cdot (σοκολάτα + κουπόνι)$
όπου "σοκολάτα" εδώ είναι απλά η συντομογραφία για την ποσότητα της πραγματικής σοκολάτας σε μια μπάρα.
Όμως, το ίδιο το κουπόνι μέσα στην παρένθεση αξίζει $\frac{1}{4}$ της μπάρας, οπότε μπορούμε να γράψουμε ότι το $1$ κουπόνι αξίζει:
$\frac{1}{4} \cdot [σοκολάτα + \frac{1}{4} \cdot (σοκολάτα+κουπόνι)]$
ή αλλιώς
$\frac{1}{4} \cdot σοκολάτα + \frac{1}{16} \cdot (σοκολάτα+κουπόνι)]$
Και αν αντικαταστήσουμε πάλι το $κουπόνι$ με $\frac{1}{4} \cdot (σοκολάτα + κουπόνι)$ παίρνουμε:
$\frac{1}{4} \cdot σοκολάτα + \frac{1}{16} \cdot[ σοκολάτα+\frac{1}{4} \cdot (σοκολάτα+κουπόνι) ]$
Και αν συνεχίσουμε έτσι για πάντα, θα διαπιστώσουμε ότι $1$ κουπόνι αξίζει
$(\frac{1}{4}+\frac{1}{16}+\frac{1}{64} + \cdots) \cdot σοκολάτα $
ή πιο απλά:
$(\frac{1}{4}+\frac{1}{16}+\frac{1}{64} + \cdots) $ μονάδες πραγματικής σοκολάτας.
Για να αποδείξουμε το αποτέλεσμά μας, λοιπόν, πρέπει απλώς να αποδείξουμε ότι $1$ κουπόνι αξίζει επίσης $\frac{1}{3}$ μονάδα πραγματικής σοκολάτας.
Σε αναζήτηση του 1/3
Για να το θέσουμε αλλιώς, πρέπει να αποδείξουμε ότι $3$ κουπόνια αξίζουν $1$ μονάδα πραγματικής σοκολάτας. Και για να το κάνετε αυτό, φανταστείτε ότι κάποιος έχει μαζέψει $3$ κουπόνια, έρχεται στο κατάστημα σας και λέει:
"Καλημέρα. Θα ήθελα να αγοράσω μια σοκολάτα. Σκοπεύω να φάω τη σοκολάτα αμέσως, στο μαγαζί σας, και θα σας πληρώσω όταν την έχω φάει".
Η πρώτη σας σκέψη θα είναι αναμφίβολα «άλλος ένας τρελός μαθηματικός!» αλλά ας πούμε ότι του δίνετε όντως μια σοκολάτα. Εκείνος ανοίγει και τρώει τη σοκολάτα. Στη συνέχεια, βγάζει το κουπόνι που ήταν μέσα στη σοκολάτα, το προσθέτει στα $3$ που έχει ήδη, έτσι ώστε να έχει τώρα $4$ κουπόνια. Επειτα, τα παρουσιάζει όλα μαζί και σας λέει:
«Εδώ είναι 4 κουπόνια. Δικαιούμαι μια σοκολάτα!»
Σε αυτό το σημείο, προφανώς εσείς του λέτε:
«Έχεις κοντή μνήμη, έτσι δεν είναι; Μόλις σου έδωσα μια σοκολάτα!»
Κάπως αμήχανα, εκείνος απαντά:
«Φυσικά και έχεις δίκιο. Πόσο ανόητο εκ μέρους μου. Οπότε δε μου χρωστάς τίποτα, και ούτε εγώ σου χρωστάω τίποτα. Σας ευχαριστώ πολύ. Καλημέρα!»
Δηλαδή ο πελάτης αυτός ήρθε στο κατάστημά σας με $3$ κουπόνια και χωρίς σοκολάτα και έφυγε χωρίς κουπόνια και με 1 μονάδα σοκολάτας στο στομάχι του. Άρα, τα $3$ κουπόνια του άξιζαν τελικά όσο μια μονάδα σοκολάτας, επομένως το $1$ κουπόνι αξίζει $\frac{1}{3}$ μονάδα πραγματικής σοκολάτας!
Επομένως, δείξαμε ότι:
$(\frac{1}{4}+\frac{1}{16}+\frac{1}{64} + \cdots) = \frac{1}{3} $
Ό,τι κι αν σκεφτείτε για αυτήν την ασυνήθιστη... απόδειξη, το αποτέλεσμα περιέχει μια πολύ σημαντική ιδέα:
Είναι δυνατόν άπειροι θετικοί αριθμοί να έχουν πεπερασμένο άθροισμα.
Αντί επιλόγου: Τι είναι οι σειρές
Στα μαθηματικά ονομάζουμε σειρά το άθροισμα των όρων μιας ακολουθίας αριθμών. Οι σειρές διαχωρίζονται σε πεπερασμένες και άπειρες, στις πρώτες έχουν ορισθεί ο πρώτος και ο τελευταίος όρος, ενώ στις άπειρες σειρές οι όροι συνεχίζονται επ' αόριστον, δηλαδή το πλήθος των όρων είναι άπειρο, όπως στη σειρά που μελετήσαμε εδώ. Σε αντίθεση με πεπερασμένα αθροίσματα, οι άπειρες σειρές χρειάζονται εργαλεία από τη μαθηματική ανάλυση, και συγκεκριμένα την έννοια των ορίων, για να γίνουν πλήρως κατανοητές και να μπορέσουν να χρησιμοποιηθούν. Εκτός από την παρουσία τους στα μαθηματικά, οι άπειρες σειρές χρησιμοποιούνται ευρέως και σε άλλες επιστήμες όπως η φυσική, η επιστήμη των υπολογιστών και η επιστήμη των χρηματοοικονομικών.
Πηγή άρθρου: Αυτό το άρθρο αποτελεί απόσπασμα από το νέο βιβλίο του David Acheson "The spirit of mathematics", που κυκλοφορεί από τον εκδοτικό οίκο Oxford University Press.