Μια απλή γεωμετρική ιδέα έχει χρησιμοποιηθεί για να τροφοδοτήσει τις εξελίξεις στη θεωρία της πληροφορίας, την κρυπτογραφία ακόμη και την τεχνολογία blockchain.
Δεδομένου ενός συνόλου σημείων στο χώρο, μπορείτε να βρείτε έναν ορισμένο τύπο καμπύλης που να διέρχεται από όλα αυτά; Το ερώτημα αυτό, μια εκδοχή αυτού που ονομάζεται πρόβλημα παρεμβολής, έχει απασχολήσει τους μαθηματικούς από την αρχαιότητα. Νωρίτερα φέτος, οι μαθηματικοί Eric Larson και Isabel Vogt το έλυσαν πλήρως. Αλλά ενώ η εργασία αυτή έχει προκαλέσει μεγάλο ενθουσιασμό στους “θεωρητικούς” μαθηματικούς, η παρεμβολή έχει πρακτικές συνέπειες που εκτείνονται πολύ πέρα από το πεδίο της γεωμετρίας. Η παρεμβολή έχει κεντρική σημασία για την αποθήκευση και την επικοινωνία ηλεκτρονικών δεδομένων, την κατασκευή κρυπτογραφικών συστημάτων και πολλά άλλα. Αυτός είναι ο λόγος για τον οποίο μπορείτε να γρατζουνίσετε ένα CD και να εξακολουθείτε να ακούτε μουσική, ή να λερώσετε έναν κωδικό QR και να τον σαρώσετε. Αυτός είναι επίσης ο λόγος για τον οποίο διαστημικές αποστολές όπως το πρόγραμμα Voyager μπορούσαν να στείλουν καθαρές ψηφιακές εικόνες στη Γη. Κι αυτός είναι ο λόγος για τον οποίο ένα δίκτυο υπολογιστών μπορεί να εκτελέσει έναν πολύπλοκο υπολογισμό ακόμη και αν ένας από αυτούς τους υπολογιστές παρουσιάσει βλάβη. Όλες αυτές οι εφαρμογές βασίζονται σε μια εντυπωσιακά όμορφη και απλή χρήση της παρεμβολής: τους λεγόμενους κώδικες Reed-Solomon και τους κώδικες που βασίζονται σε αυτούς.
Σημείο προς σημείο
Ας πούμε ότι θέλετε να στείλετε ένα μήνυμα που αποτελείται από δύο αριθμούς: 2 και 7. Είναι πιθανό κάποια από τα δεδομένα που μεταδίδετε να χαθούν ή να καταστραφούν πχ το 2 μπορεί να μετατραπεί σε -2. Έτσι, αντί να στέλνετε απλώς τα δεδομένα, μπορείτε να προσθέσετε επιπλέον πληροφορίες για να βοηθήσετε τον παραλήπτη να εντοπίσει και να διορθώσει τα σφάλματα που ενδέχεται να προκύψουν. Αυτό ονομάζεται κώδικας διόρθωσης σφαλμάτων.
Το απλούστερο παράδειγμα ενός τέτοιου κώδικα περιλαμβάνει τη μετάδοση του ίδιου μηνύματος πολλές φορές. Για να μπορέσει ο παραλήπτης να εντοπίσει αν συνέβη σφάλμα, στείλτε το ίδιο μήνυμα δύο φορές: 2, 7, 2, 7. Αν οι αριθμοί στις αντίστοιχες θέσεις δεν ταιριάζουν (π. χ. αν η μετάδοση γράφει 2, 7, -2, 7), ο παραλήπτης θα ξέρει ότι ένας από αυτούς είναι λάθος, αλλά όχι ποιος. Για να το καταλάβουν και να διορθώσουν το λάθος, στείλτε το ίδιο μήνυμα τρεις φορές: 2, 7, 2, 7, 2, 7, 2, 7. Ο παραλήπτης πρέπει απλώς να πάρει την πλειοψηφία για να καταλάβει το μήνυμα που θέλετε να στείλετε.
Ωστόσο αυτό το μέσο διόρθωσης των σφαλμάτων είναι εξαιρετικά αναποτελεσματικό. Υπάρχει μια πιο έξυπνη προσέγγιση: Κωδικοποιήστε το μήνυμα ως γεωμετρική καμπύλη και στείλτε μόνο όσες πληροφορίες χρειάζονται για να μπορέσει ο παραλήπτης να ανακατασκευάσει αυτή την καμπύλη!
Στην απλή μας περίπτωση μετάδοσης 2 και 7, η καμπύλη θα είναι η ευθεία $ y = 2x + 7 $. Υπολογίστε την καμπύλη αυτή σε δύο προκαθορισμένες τιμές του x και μεταδώστε τις τιμές y που προκύπτουν. Ο παραλήπτης έχει τώρα δύο σημεία και επειδή το πρόβλημα παρεμβολής μας λέει ότι δύο σημεία προσδιορίζουν μια μοναδική ευθεία, ο παραλήπτης πρέπει απλώς να βρει την ευθεία που διέρχεται από τα σημεία που έλαβε. Με δύο λόγια, οι συντελεστές της εξίσωσης αποκαλύπτουν το επιδιωκόμενο μήνυμα.
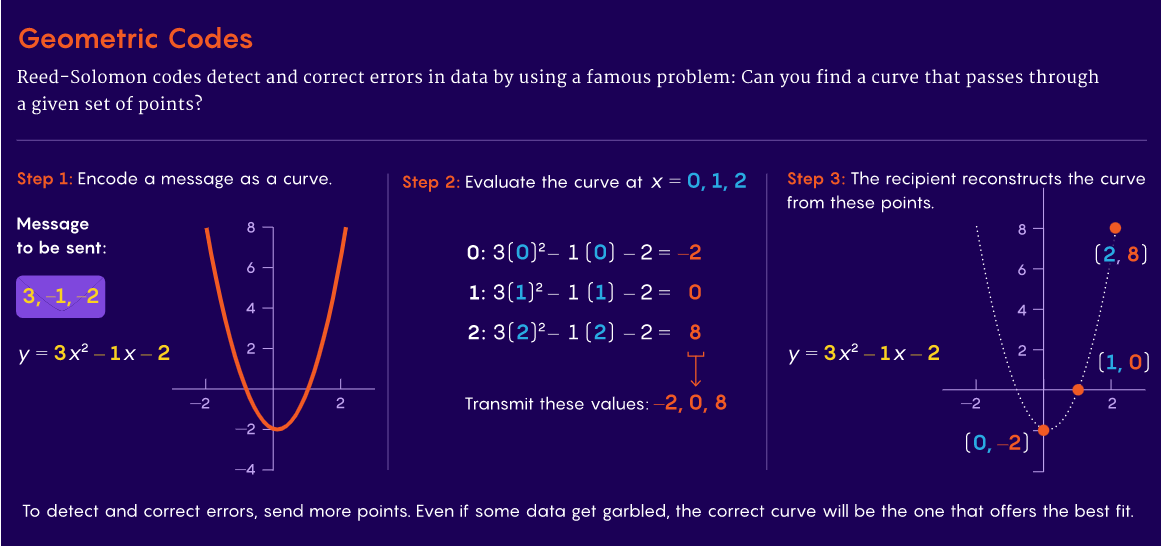
Για να αποφύγετε τα σφάλματα, προσθέτετε και πάλι επιπλέον πληροφορίες. Εδώ, στέλνετε την τιμή y που αντιστοιχεί σε μια άλλη προκαθορισμένη συντεταγμένη x. Εάν τα τρία σημεία δεν εμπίπτουν στην ίδια γραμμή, υπάρχει σφάλμα. Και για να καταλάβετε πού βρίσκεται το σφάλμα, στέλνετε απλώς μία ακόμη τιμή δηλαδή έχετε στείλει συνολικά τέσσερις αριθμούς αντί για έξι που απαιτούσε η προηγούμενη μέθοδος. Το πλεονέκτημα αυξάνεται με το μέγεθος του μηνύματος. Ας πούμε ότι θέλετε να στείλετε ένα μεγαλύτερο μήνυμα, 1.000 αριθμούς. Ο λιγότερο αποδοτικός κώδικας θα απαιτούσε την αποστολή 2.000 αριθμών για να εντοπιστεί ένα σφάλμα και 3.000 αριθμών για να διορθωθεί. Αν όμως χρησιμοποιήσετε τον κώδικα που περιλαμβάνει την παρεμβολή ενός πολυωνύμου μέσω συγκεκριμένων σημείων, χρειάζεστε μόνο 1.001 αριθμούς για να βρείτε το σφάλμα και 1.002 για να το διορθώσετε! Μπορείτε βέβαια να προσθέσετε περισσότερα σημεία για να εντοπίσετε και να διορθώσετε περισσότερα πιθανά λάθη. Όμως όσο αυξάνεται το μήκος του μηνύματός σας, η διαφορά απόδοσης μεταξύ των δύο κωδίκων γίνεται όλο και μεγαλύτερη.
Ο αποδοτικότερος κώδικας ονομάζεται κώδικας Reed-Solomon. Από την εισαγωγή του το 1960, οι μαθηματικοί έχουν κάνει περαιτέρω ανακαλύψεις, αναπτύσσοντας αλγορίθμους που μπορούν να διορθώνουν περισσότερα λάθη με μεγαλύτερη αποτελεσματικότητα. "Είναι πολύ κομψό, καθαρό, συγκεκριμένο", δήλωσε ο Swastik Kopparty, μαθηματικός και επιστήμονας υπολογιστών στο Πανεπιστήμιο του Τορόντο. "Μπορεί να διδαχθεί σε έναν δευτεροετή προπτυχιακό φοιτητή σε μισή ώρα".
Οι κώδικες Reed-Solomon ήταν ιδιαίτερα χρήσιμοι για την αποθήκευση και τη μετάδοση πληροφοριών ηλεκτρονικά. Αλλά η ίδια έννοια ήταν επίσης απαραίτητη στην κρυπτογραφία και την κατανεμημένη πληροφορική. Ας πάρουμε την κοινή χρήση μυστικών: Ας υποθέσουμε ότι θέλετε να διανείμετε ένα μυστικό σε διάφορα μέρη, έτσι ώστε κανένα άτομο να μην μπορεί να έχει πρόσβαση σε ολόκληρο το μυστικό, αλλά όλοι μαζί μπορούν. (Φανταστείτε ένα κλειδί κρυπτογράφησης, για παράδειγμα, ή έναν κωδικό εκτόξευσης πυραύλων). Κωδικοποιείτε τους αριθμούς σε ένα πολυώνυμο, αξιολογείτε αυτό το πολυώνυμο σε ένα προκαθορισμένο σύνολο σημείων και διανέμετε καθένα από τα αποτελέσματα σε διαφορετικό άτομο.
Πιο πρόσφατα, οι κώδικες Reed-Solomon έχουν χρησιμοποιηθεί σε τομείς όπως το cloud computing και η τεχνολογία blockchain. Ας πούμε ότι πρέπει να εκτελέσετε έναν υπολογισμό που είναι πολύ περίπλοκος για τον φορητό σας υπολογιστή, οπότε τον εκτελεί ένα μεγάλο υπολογιστικό σύμπλεγμα, αλλά τώρα πρέπει να επαληθεύσετε ότι ο υπολογισμός που θα λάβετε πίσω είναι σωστός. Οι κώδικες Reed-Solomon σας επιτρέπουν να ζητήσετε πρόσθετες πληροφορίες που η συστάδα πιθανόν να μην είναι σε θέση να παράγει αν δεν έχει κάνει σωστά τον υπολογισμό.

Αλλά οι κώδικες Reed-Solomon έχουν επίσης έναν σημαντικό περιορισμό. Κατασκευάζονται με τέτοιο τρόπο ώστε να μπορείτε να αξιολογήσετε το πολυώνυμό σας μόνο σε ένα σταθερό (και συνήθως σχετικά μικρό) σύνολο τιμών. Δηλαδή, περιορίζεστε στη χρήση ενός συγκεκριμένου συνόλου αριθμών για την κωδικοποίηση του μηνύματός σας. Το μέγεθος αυτού του συνόλου, ή αλφάβητου, περιορίζει με τη σειρά του το μήκος των μηνυμάτων που μπορείτε να στείλετε και όσο μεγαλύτερο είναι το αλφάβητό σας, τόσο περισσότερη υπολογιστική ισχύ θα χρειαστείτε για την αποκωδικοποίηση αυτών των μηνυμάτων. Και έτσι οι μαθηματικοί αναζήτησαν έναν ακόμη πιο βέλτιστο κώδικα.
Μελλοντικοί Κώδικες
Ένας πιο γενικός, πιο ισχυρός κώδικας θα σας επέτρεπε να αποθηκεύετε ή να στέλνετε μεγαλύτερα μηνύματα χωρίς να χρειάζεται να αυξήσετε το μέγεθος του αλφαβήτου σας. Για να γίνει αυτό, οι μαθηματικοί επινόησαν κώδικες που περιλαμβάνουν την παρεμβολή μιας συνάρτησης η οποία ζει σε έναν ειδικό χώρο που συνδέεται με μια πιο περίπλοκη καμπύλη, μέσω συγκεκριμένων σημείων της καμπύλης αυτής. Αυτοί οι λεγόμενοι κώδικες αλγεβρικής γεωμετρίας "εμφανίστηκαν από το πουθενά και είναι καλύτεροι από οποιονδήποτε άλλο κώδικα που ξέρουμε να φτιάξουμε με μικρότερο αλφάβητο", δήλωσε ο Kopparty. "Αυτό ξεπερνάει τα πάντα. Ήταν ένα πραγματικό σοκ".
Υπάρχει μόνο ένα πρόβλημα. Στην πράξη, η υλοποίηση ενός κώδικα Reed-Solomon είναι πολύ, πολύ πιο εύκολη από την υλοποίηση ενός κώδικα αλγεβρικής γεωμετρίας. "Πρόκειται για την τελευταία λέξη της τεχνολογίας, αλλά είναι ακόμη υπό έρευνα για να μετατραπεί πραγματικά σε κάτι πρακτικό", δήλωσε ο κρυπτολόγος Simon Abelard. "Πρόκειται για αρκετά αφηρημένα μαθηματικά και είναι δύσκολο να χειριστείς αυτούς τους κώδικες σε έναν υπολογιστή".
Προς το παρόν, αυτό δεν είναι ανησυχητικό: σε πραγματικές εφαρμογές, οι κώδικες Reed-Solomon και οι συναφείς μορφές διόρθωσης σφαλμάτων είναι επαρκείς. Αλλά αυτό μπορεί να μην ισχύει πάντα. Για παράδειγμα, αν στο μέλλον καταστούν διαθέσιμοι ισχυροί κβαντικοί υπολογιστές, θα είναι σε θέση να σπάσουν τα σημερινά πρωτόκολλα κρυπτογράφησης. Ως εκ τούτου, οι ερευνητές αναζητούν σχήματα που μπορούν να αντισταθούν σε κβαντικές επιθέσεις...
