Σε αυτό το κείμενο μπορείτε να μάθετε με απλά λόγια όλα όσα πρέπει να ξέρετε για την κβαντοδυναμική, μια θεμελιωμένη θεωρία της φυσικής. Ας δούμε με απλά λόγια λοιπόν τι είναι αυτή η θεωρία.
Τι είναι η κβαντική φυσική;
Η κβαντική φυσική είναι ένας κλάδος της φυσικής επίσης γνωστής ως κβαντική μηχανική ή κβαντική θεωρία.
Η μηχανική, είναι εκείνο το μέρος της φυσικής που ασχολείται με πράγματα που μετακινούνται (μπάλες του τένις, αυτοκίνητα, ρουκέτες πλανήτες κλπ.). Παράλληλα, περιγράφει τις κινήσεις των αντικειμένων σε μοριακά, ατομικά και υποατομικά επίπεδα, όπως φωτόνια και ηλεκτρόνια.
Παρόλο που θεωρείται μια εξαιρετικά επιτυχημένη επιστημονική θεωρία, στην οποία βασίζεται μεγάλο μέρος του σύγχρονου τρόπου ζωής μας, θα μπορούσαμε να την χαρακτηρίσουμε κάπως... περίπλοκη.
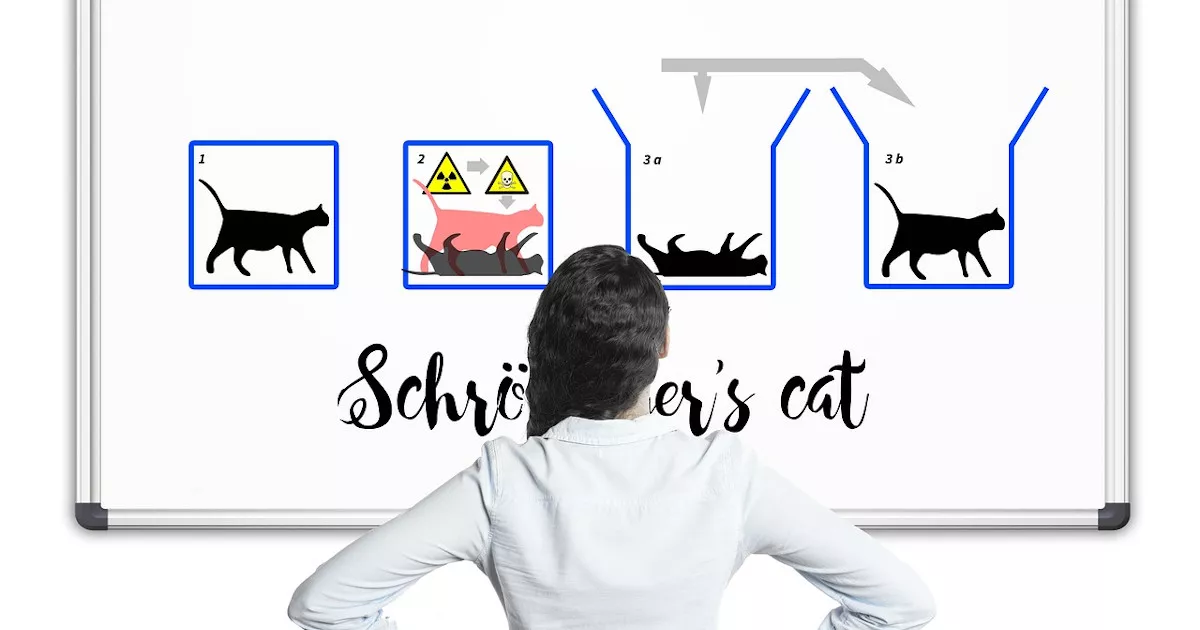
Υπάρχουν διάφορες μαθηματικές θεμελιώσεις της κβαντικής μηχανικής, όπως και πειράματα. Χαρακτηριστικότερο από αυτά τα πειράματα είναι εκείνο της γάτας του Σρέντινγκερ. Πρόκειται για ένα νοητικό αυτό πείραμα, που δημιουργήθηκε από τον Αυστριακό φυσικό Έρβιν Σρέντινγκερ το 1935. Το σενάριο παρουσιάζει μια γάτα, η οποία μπορεί να είναι ταυτόχρονα ζωντανή και νεκρή, με την κατάστασή της να συνδέεται με προηγούμενο τυχαίο γεγονός.
Σύμφωνα με τον Σρέντινγκερ, μια γάτα τοποθετείται σε ένα κουτί με ένα φιαλίδιο δηλητηρίου, το οποίο θα σπάσει αυτόματα εάν αποσυντεθεί ένα ραδιενεργό σωματίδιο. Η ραδιενεργή διάσπαση είναι μία από τις πτυχές της κβαντικής φυσικής βάσει της πιθανότητας. Δεν μπορούμε να πούμε πότε ένα δεδομένο σωματίδιο θα αποσυντεθεί, γνωρίζουμε μόνο την πιθανότητα αποσύνθεσης σε μια συγκεκριμένη περίοδο. Αφού παρέλθει κάποιος χρόνος, ένα μη παρατηρημένο σωματίδιο θα βρίσκεται σε υπέρθεση αποσυντεθειμένων και μη αποσυντεθειμένων καταστάσεων. Το μόνο που υπάρχει πριν από τη μέτρηση (όταν κάποιος κοιτάζει μέσα στο κουτί) είναι οι πιθανότητες. Αλλά επειδή η ζωή της γάτας εξαρτάται από την κατάσταση του σωματιδίου, αυτό σημαίνει ότι η γάτα είναι ταυτόχρονα νεκρή και ζωντανή;
Στην πραγματικότητα, δεν θα μπορούσαμε ποτέ να δούμε τη γάτα να είναι ζωντανή και νεκρή. Μόλις κοιτάξουμε στο κουτί, η γάτα θα είναι σε μία μόνο κατάσταση. Εξάλλου, οι πρακτικές λεπτομέρειες του πειράματος δεν το επιτρέπουν. Για να μπορέσει ο ανιχνευτής να απελευθερώσει το δηλητήριο θα πρέπει να αλληλοεπιδράσει με το σωματίδιο, αναγκάζοντας τον είτε να αποσυντεθεί είτε να μην αποσυντεθεί.
Παρά τους περιορισμούς της, η γάτα του Σρέντινγκερ μας δίνει μια αίσθηση για το πολύπλοκο θέμα της υπέρθεσης. Η θεωρία προφανώς λειτουργεί, αφήνοντας μας όμως να κυνηγάμε φαντάσματα, σωματίδια γάτες που είναι ταυτόχρονα ζωντανές και νεκρές και πολλά άλλα φαινομενικά τρομακτικά πράγματα.
Εάν βρίσκετε τη κβαντική θεωρία όντως περίπλοκη, αλλά θέλετε να μάθετε κι άλλα γι' αυτήν ώστε να ξεδιαλύνετε τα μυστήριά της, δεν έχετε παρά να διαβάσετε παρακάτω.
Η ιστορία της κβαντικής μηχανικής
Σήμερα γνωρίζουμε πολύ καλά ότι η ύλη αποτελείται από άτομα. Κάθε άτομο αποτελείται με τη σειρά του από ηλεκτρόνια που «περιστρέφονται» σε τροχιά γύρω από έναν πυρήνα που αποτελείται από πρωτόνια και νετρόνια. Τα άτομα είναι διακριτά. Είναι «εντοπισμένα»: «εδώ» ή «εκεί». Προς το τέλος του 19ου αιώνα, όμως, τα άτομα ήταν πραγματικά αμφιλεγόμενα. Στην προσπάθειά του να αντικρούσει την ύπαρξη των ατόμων, ο γερμανικός φυσικός Μαξ Πλανκ, οδηγήθηκε στο να μελετήσει τις ιδιότητες και τη συμπεριφορά της λεγόμενης ακτινοβολίας "μαύρου σώματος".
Προς το τέλος του 1900, ο Πλανκ κατέληξε στο συμπέρασμα ότι η ακτινοβολία απορροφάται και εκπέμπεται σαν να αποτελείται από διακριτά κομμάτια, τα οποία ονόμασε κβάντα. Το 1905, ο Άλμπερτ Αϊνστάιν προχώρησε περισσότερο. Είπε ότι τα κβάντα είναι η ίδια η ακτινοβολία που έρχεται σε διακριτά κομμάτια φωτεινής ενέργειας. Σήμερα τα ονομάζουμε "συσσωρευμένα φωτόνια".
Το φως είναι κύμα η σωματίδιο;
Η υπόθεση του Αϊνστάιν έθεσε προβληματισμούς. Υπήρχε ένα ήδη καθιερωμένο σώμα αποδεικτικών στοιχείων υπέρ μιας θεωρίας κυμάτων του φωτός. Η βασική παρατήρηση ονομάζεται «πείραμα διπλής σχισμής».
Σύμφωνα με το πείραμα αυτό, αφού σπρώξουμε το φως μέσα από ένα στενό άνοιγμα ή σχισμή, θα συμπιεστεί, θα λυγίσει στα άκρα και θα απλωθεί. Το ίδιο θα συμβεί, εάν κόψουμε δύο σχισμές δίπλα-δίπλα. Θα έχουμε παρεμβολές. Τα κύματα που διαθλάσσονται από τις δύο σχισμές παράγουν ένα εναλλασσόμενο μοτίβο ελαφριών και σκοτεινών ζωνών που ονομάζονται περιθώρια παρεμβολής. Αυτό το είδος συμπεριφοράς δεν περιορίζεται στο φως.
Η υπόθεση του Αϊνστάιν, δεν ανέτρεψε όλα τα στοιχεία για τις μετατοπισμένες κυματοειδείς ιδιότητες του φωτός. Αυτό που πρότεινε είναι ότι μια ολοκληρωμένη περιγραφή πρέπει να λάβει υπόψη και τις τοπικές, σωματιδιακές ιδιότητές της. Έτσι, το φως ενεργεί σαν ένα κύμα και ένα σωματίδιο.
Το 1923, ο Γάλλος φυσικός Λουί ντε Μπρέιγ έκανε μια τολμηρή πρόταση. Εάν τα κύματα φωτός μπορούν επίσης να είναι σωματίδια, θα μπορούσαν τα σωματίδια να είναι κύματα όπως τα ηλεκτρόνια; Αυτή ήταν απλώς μια ιδέα, η οποία όμως χρησιμοποιήθηκε για να αναπτύξει μια άμεση μαθηματική σχέση μεταξύ μιας ιδέας που μοιάζει με κύμα ενός ηλεκτρονίου (μήκος κύματος) και μιας ιδιότητας τύπου σωματιδίων (ορμή).
Αλλά αυτό δεν ήταν μια ολοκληρωμένη θεωρία "κυμάτων-σωματιδίων" της ύλης. Αυτή η πρόκληση, έπεσε στον Έρβιν Σρέντινγκερ, του οποίου η διατύπωση (που δημοσιεύθηκε για πρώτη φορά στις αρχές του 1926 και ονομάζεται κυματομηχανική) εξακολουθεί να διδάσκεται στους φοιτητές της επιστήμης μέχρι σήμερα.
Τι είναι η λειτουργία κύματος;
Η θεωρία του Σρέντινγκερ, είναι πραγματικά η κλασική θεωρία των κυμάτων στην οποία εισάγουμε κάποιες κβαντικές συνθήκες χρησιμοποιώντας τη σχέση του Ντε Μπρέιγ. Το αποτέλεσμα είναι η εξίσωση κυμάτων του Σρέντινγκερ, στην οποία υπολογίζεται η κίνηση ενός σωματιδίου όπως ένα ηλεκτρόνιο από τη λειτουργία του κύματος.
Στην κλασική μηχανική, δεν υπάρχουν ζητήματα σχετικά με τον τρόπο ερμηνείας των εννοιών που αντιπροσωπεύονται στη θεωρία, όπως η ενέργεια και η ορμή και η σχέση τους με τις ιδιότητες των αντικειμένων που τα κατέχουν.
Θέλουμε πχ να υπολογίσουμε την κλασική ορμή ενός αντικειμένου που πετάει στον αέρα με σταθερή ταχύτητα; Δεν έχουμε παρά να μετρήσουμε τη μάζα του αντικειμένου, την ταχύτητά του και έπειτα να τα πολλαπλασιάσουμε.
Τι γίνεται όμως αν θέλουμε να μάθουμε την ορμή ενός ηλεκτρονίου που κινείται ελεύθερα σε κενό; Στην κβαντική μηχανική το υπολογίζουμε εκτελώντας μια συγκεκριμένη μαθηματική λειτουργία, στη λειτουργία κύματος του ηλεκτρονίου.
Αυτές τις λειτουργίες, μπορούμε να τις σκεφτούμε ως “κλειδιά” τα οποία ξεκλειδώνουν την λειτουργία κύματος, απελευθερώνοντας το παρατηρήσιμο πριν κλείσει ξανά.
Τα σωματίδια συμπεριφέρονται πραγματικά σαν κύματα;
Αν τα ηλεκτρόνια συμπεριφέρονται σαν κύματα, μπορούν να διαθλαστούν;. Αν σπρώξουμε μια δέσμη ηλεκτρονίων μέσα από δύο σχισμές δίπλα-δίπλα θα δούμε παρεμβολές σε μια μακρινή οθόνη; Κι αν περιορίσουμε την ένταση της ακτίνας έτσι ώστε κατά μέσο όρο, μόνο ένα ηλεκτρόνιο να περνάει μέσα από τις σχισμές κάθε φορά. Τι θα γίνει τότε;
Αυτό που βλέπουμε, είναι στην αρχή αρκετά παρήγορο. Κάθε ηλεκτρόνιο που διέρχεται από τις σχισμές καταγράφεται ως ένα ενιαίο σημείο στην οθόνη, λέγοντάς μας ότι «ένα ηλεκτρόνιο χτύπησε εδώ». Αυτό είναι απολύτως σύμφωνο με την έννοια των ηλεκτρονίων ως σωματίδια, καθώς φαίνεται ότι περνούν, ένα προς ένα, από τις σχισμές και χτυπούν την οθόνη σε ένα φαινομενικά τυχαίο μοτίβο.
Το μοτίβο όμως δεν είναι τυχαίο. Καθώς όλο και περισσότερα ηλεκτρόνια περνούν από τις σχισμές, διασχίζουμε ένα κατώφλι. Αρχίζουμε να βλέπουμε μεμονωμένες κουκκίδες μαζί, να επικαλύπτονται και να συγχωνεύονται. Τελικά έχουμε ένα μοτίβο παρεμβολών δύο σχισμών με εναλλασσόμενα φωτεινά και σκοτεινά περιθώρια.
Εναλλακτικά, συμπεραίνουμε ότι η κυματική φύση του ηλεκτρονίου είναι εγγενής συμπεριφορά. Κάθε μεμονωμένο ηλεκτρόνιο συμπεριφέρεται ως κύμα, που περιγράφεται από μια λειτουργία κύματος, περνώντας ταυτόχρονα και από τις δύο σχισμές, παρεμβαίνοντας στον εαυτό του πριν χτυπήσει την οθόνη.
Επομένως, πώς πρέπει να γνωρίζουμε ακριβώς πού θα εμφανιστεί το επόμενο ηλεκτρόνιο;
Μπορεί ένα σωματίδιο να βρίσκεται σε δύο μέρη ταυτόχρονα;
Ο Σρέντινγκερ, ήθελε να ερμηνεύσει κυριολεκτικά τη λειτουργία κυμάτων, ως θεωρητική αναπαράσταση ενός «κύματος ύλης». Αλλά για να κατανοήσουμε την παρεμβολή ενός ηλεκτρονίου πρέπει να επιτύχουμε μια εναλλακτική ερμηνεία που προτάθηκε αργότερα το 1926 από τον Μαξ Μπορν.
Ο Μαξ Μπορν, πίστευε ότι στην κβαντική μηχανική η λειτουργία κύματος είναι ένα μέτρο της πιθανότητας «εύρεσης» του σχετικού ηλεκτρονίου σε ένα ορισμένο σημείο.
Οι εναλλασσόμενες κορυφές και κοιλότητες του κύματος ηλεκτρονίων μεταφράζονται σε ένα μοτίβο κβαντικών πιθανοτήτων. Σε αυτήν την τοποθεσία (η οποία θα γίνει μια φωτεινή περιφέρεια) υπάρχει μεγαλύτερη πιθανότητα εύρεσης του επόμενου ηλεκτρονίου και στην άλλη θέση (η οποία θα γίνει ένα σκοτεινό περιθώριο ) υπάρχει πολύ χαμηλή ή μηδενική πιθανότητα εύρεσης του επόμενου ηλεκτρονίου.
Πριν ένα ηλεκτρόνιο χτυπήσει την οθόνη, έχει την πιθανότητα να βρεθεί «εδώ», «εκεί» και «οπουδήποτε» όπου το τετράγωνο της λειτουργίας κύματος είναι μεγαλύτερο από το μηδέν. Αυτή η πιθανότητα πολλών καταστάσεων που υπάρχουν ταυτόχρονα είναι γνωστή ως «κβαντική υπέρθεση».
Αυτό σημαίνει ότι ένα μεμονωμένο ηλεκτρόνιο μπορεί να είναι σε περισσότερα από ένα μέρος κάθε φορά; Όχι, ακριβώς. Η αλήθεια είναι ότι έχει την πιθανότητα να βρεθεί σε περισσότερα από ένα μέρος κάθε φορά.
Γιατί είναι σημαντική η πιθανότητα στην κβαντική φυσική;
Ένα κλασικό παράδειγμα πιθανοτήτων είναι το κλασικό παράδειγμα της ρίψης του νομίσματος (κορώνα ή γράμματα). Καθώς το νόμισμα, περιστρέφεται στον αέρα, δεν γνωρίζουμε τις ακριβείς λεπτομέρειες της κίνησής του, οπότε δεν μπορούμε να προβλέψουμε με βεβαιότητα ποια πλευρά θα προσγειωθεί προς τα πάνω.
Η κβαντική πιθανότητα διαφέρει. Όταν πετάμε ένα κβαντικό νόμισμα, στην πραγματικότητα θα μπορούσαμε να γνωρίζουμε πολύ καλά τις περισσότερες λεπτομέρειες της κίνησής του, αλλά δεν μπορούμε να υποθέσουμε ότι κορώνα ή γράμματα υπάρχουν πριν από την προσγείωση του νομίσματος.
Ο Αϊνστάιν αποδοκίμασε αυτό το φαινομενικό στοιχείο της καθαρής τύχης στην κβαντική μηχανική. Δήλωσε μάλιστα πως "Ο Θεός δεν παίζει ζάρια".
Το άρθρο προέρχεται από άρθρο του Jim Baggott στο Science Focus Magazine του BBC. Δείτε εδώ το link από όπου μπορείτε να αγοράσετε το βιβλίο του, Quantum Reality: The Quest for the Real Meaning of Quantum Mechanics – a Game of Theories:
https://global.oup.com/academic/product/quantum-reality-9780198830153?cc=gb&lang=en&